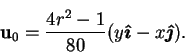Next: First order mass fraction
Up: Spherical enclosures
Previous: Conduction-diffusion
Contents
The solution for 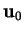 and
and 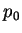 (creeping flow)
is obtained by the method of §B.4.
(creeping flow)
is obtained by the method of §B.4.
Here the body force is
The scalar defining its scaloidal part satisfies
This is
![\begin{displaymath}
\mbox{$\mathcal S$}[\mathbf{f}_0] = -\frac{1}{4}r^2\sin^2\theta\sin 2\phi,
\end{displaymath}](img1087.png) |
(8.33) |
so that
and
which is obviously solenoidal, as expected.
Clearly
![\begin{displaymath}
\mbox{$\mathcal P$}[\mathbf{f}_0-\mathbf{f}_0^{(S)}] = 0,
\end{displaymath}](img1093.png) |
(8.36) |
since
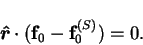 |
(8.37) |
The problem for the scalar defining the toroidal part of the body force is:
The solution is
![$\displaystyle \mbox{$\mathcal T$}[\mathbf{f}_0-\mathbf{f}_0^{(S)}] = -\frac{1}{2}r\cos\theta.$](img1098.png) |
|
|
(8.40) |
To illustrate the decomposition of the vector field here, the force-lines
of 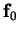 ,
,
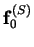 and
and
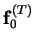 in
the plane
in
the plane 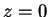 are plotted in figure 8.3.
are plotted in figure 8.3.
Figure 8.3:
Decomposition of the vector field 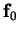 into scaloidal,
into scaloidal,
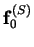 , and toroidal,
, and toroidal,
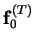 , parts. The fields
are represented by their force-lines in the plane
, parts. The fields
are represented by their force-lines in the plane  ,
the contours of
,
the contours of 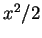 ,
, 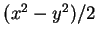 and
and 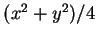 .
.
![\begin{figure}\centering\begin{picture}(120,180)(-60,-60)
\put(0,0){\makebox(0,0...
...,-50){\makebox(0,0)[br]{\LARGE$\mathbf{f}_0^{(T)}$}}
}
\end{picture}\end{figure}](img1105.png) |
Since, in this case, all
three vector fields are plane and solenoidal, the force-lines can be
represented as the contours of scalar functions. The functions are
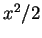 ,
, 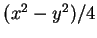 and
and 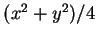 , respectively.
, respectively.
The problem for
![$\mbox{$\mathcal T$}[\mathbf{u}_0]$](img1107.png) is:
is:
The solution is:
![\begin{displaymath}
\mbox{$\mathcal T$}[\mathbf{u}_0] = \frac{r}{80}\left(1-4r^2\right)P_1^0(\cos\theta).
\end{displaymath}](img1112.png) |
(8.43) |
The other scalars,
![$\mbox{$\mathcal P$}[\mathbf{u}_0]$](img1113.png) and
and 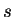 , vanish.
, vanish.
Thus,
The pressure is plotted in the plane of spanwise symmetry, 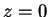 ,
in figure 8.4.
,
in figure 8.4.
Figure 8.4:
Zeroth order pressure, 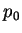 , (8.46) in the plane
, (8.46) in the plane 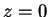 .
The maxima are in the upper-right and lower-left quadrants.
Contour levels at 0.01, 0.1(0.1)0.4, 0.6(0.1)0.9, 0.99 of range.
.
The maxima are in the upper-right and lower-left quadrants.
Contour levels at 0.01, 0.1(0.1)0.4, 0.6(0.1)0.9, 0.99 of range.
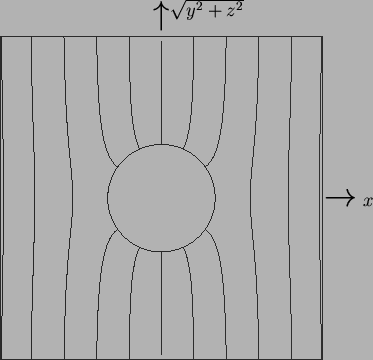 |
Since the velocity is purely toroidal, the pressure is due solely to the
scaloidal part of the body force. The force-lines of
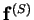 and the isobars, displayed in figures 8.3 and 8.4, are
obviously related: they are mutually orthogonal.
and the isobars, displayed in figures 8.3 and 8.4, are
obviously related: they are mutually orthogonal.
The pressure is very simply expressed in terms of Cartesian coordinates:
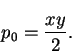 |
(8.46) |
The fact that it is independent of 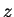 suggests--consider the spanwise
component of the equation of motion (2.54)--that
suggests--consider the spanwise
component of the equation of motion (2.54)--that  . This
is the case:
. This
is the case:
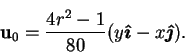 |
(8.47) |
Notice that in the horizontal plane through the centre ( )
the velocity is purely vertical and identical to the fully developed flow
in a cavity of circular horizontal section (7.65)
except for a factor of
)
the velocity is purely vertical and identical to the fully developed flow
in a cavity of circular horizontal section (7.65)
except for a factor of  .
Since
.
Since 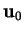 is independent of
is independent of 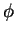 , the contours of
, the contours of
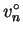 for
for
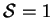 in figure 7.6 can also be interpreted as contours
of the creeping speed in any plane passing through the
in figure 7.6 can also be interpreted as contours
of the creeping speed in any plane passing through the  -axis of the sphere.
-axis of the sphere.




Next: First order mass fraction
Up: Spherical enclosures
Previous: Conduction-diffusion
Contents
Geordie McBain
2001-01-27
![]() and
and ![]() (creeping flow)
is obtained by the method of §B.4.
(creeping flow)
is obtained by the method of §B.4.
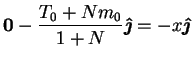
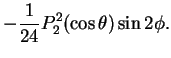
![\begin{displaymath}
\mbox{$\mathcal S$}[\mathbf{f}_0] = -\frac{1}{4}r^2\sin^2\theta\sin 2\phi,
\end{displaymath}](img1087.png)
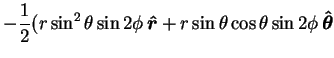
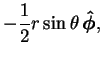
![$\displaystyle \mbox{$\mathcal T$}[\mathbf{f}_0-\mathbf{f}_0^{(S)}] = -\frac{1}{2}r\cos\theta.$](img1098.png)
![\begin{figure}\centering\begin{picture}(120,180)(-60,-60)
\put(0,0){\makebox(0,0...
...,-50){\makebox(0,0)[br]{\LARGE$\mathbf{f}_0^{(T)}$}}
}
\end{picture}\end{figure}](img1105.png)
![]() is:
is:
![$\displaystyle \mbox{$\mathcal T$}[\mathbf{f}_0-\mathbf{f}_0^{(S)}] =
-\frac{r}{2}P_1^0(\cos\theta)$](img1109.png)
![\begin{displaymath}
\mbox{$\mathcal T$}[\mathbf{u}_0] = \frac{r}{80}\left(1-4r^2\right)P_1^0(\cos\theta).
\end{displaymath}](img1112.png)
![]() ,
in figure 8.4.
,
in figure 8.4.