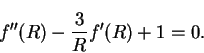Next: Elliptic section
Up: Sections other than rectangular
Previous: Sections other than rectangular
Contents
Circular section
For a circular section of diameter 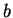 ,
,
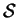 =1 and the domain is given by
=1 and the domain is given by
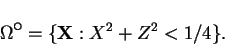 |
(7.60) |
The forced flow solution is
(Stokes 1845; Lamb 1932, p. 585; Bird et al. 1960, p. 46):
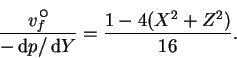 |
(7.61) |
A solution to equation (7.20) can be obtained in closed form by
transforming the independent variables 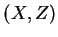 to
to 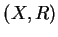 , where
, where
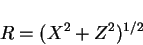 |
(7.62) |
whence it becomes apparent that (7.20) admits solutions of the
form
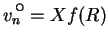 provided
provided
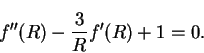 |
(7.63) |
For 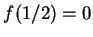 and
and  bounded as
bounded as
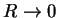 , the solution of this is:
, the solution of this is:
This solution was reported by Ostroumov (1958) for the
analogous single fluid heat transfer problem. It is also similar to the
fully developed horizontal flow in a long axially heated cylinder (Klosse &
Ullersma 1973; Bejan & Tien 1978).




Next: Elliptic section
Up: Sections other than rectangular
Previous: Sections other than rectangular
Contents
Geordie McBain
2001-01-27
![]() ,
,
![]() =1 and the domain is given by
=1 and the domain is given by
![]() to
to ![]() , where
, where