



Next: Introduction
Up: Vapour transport across gas-filled
Previous: Preface
Contents
Nomenclature
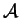
- vertical aspect ratio (reduced height) of cavity
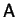
- arbitrary diffusivity tensor
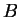
- Spalding's driving force for mass transfer,
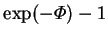
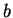
- characteristic length, dimensional width of cavity
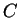
- coefficient of Dirichlet term in Robin boundary condition
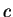
- constant of integration
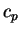
- isobaric specific heat capacity
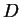
- binary diffusivity
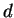
- characteristic length of
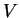 in §2.6.1
in §2.6.1
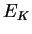
- truncation error
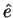
- arbitrary unit vector
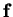
- body force term in Stokes equation
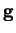
- gravitational acceleration,
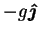
- Gr
- (thermal) Grashof number,
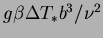
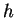
- specific enthalpy
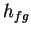
- specific heat of vaporization
- h.o.t.
- higher order terms
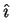
- unit transverse vector
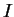
- coefficient of Neumann term in Robin boundary condition
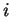
- index for species in a multicomponent mixture
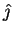
- unit vertical vector
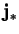
- mass flux of vapour relative to
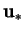
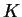
- number of evaluated terms in a truncated series
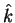
- unit spanwise vector
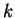
- index for terms in a series
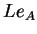
- vapour Lewis number,
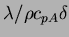
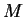
- molar mass
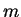
- reduced vapour mass fraction,
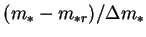
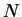
- buoyancy ratio,
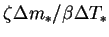 number of species in a mixture in §2.6.1
number of species in a mixture in §2.6.1
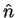
- unit normal vector, positive outward from fluid phase
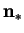
- absolute mass flux of vapour
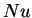
- Nusselt number,
![$-\mbox{\boldmath$\hat{\imath}$}\cdot\mathbf{e}_*b[1-\exp(-\varPhi _T)]/
\lambda\Delta T_*\varPhi _T$](img48.png)
-
![$\mbox{$\mathcal P$}[\mathbf{v}]$](img49.png)
- scalar defining the poloidal part of
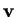
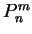
- function defined by (B.6)
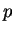
- reduced pressure,
-
-
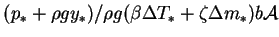
- Pr
- Prandtl number,
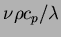
-
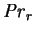
- reference Prandtl number,
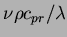
-
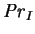
- interdiffusion Prandtl number,
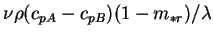
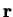
- reduced position vector,
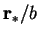
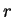
- reduced spherical coordinate,
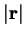
- Ra
- (thermal) Rayleigh number, GrPr
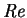
- Reynolds number
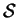
- spanwise aspect ratio (reduced span) of cavity
-
![$\mbox{$\mathcal S$}[\mathbf{v}]$](img65.png)
- scalar defining the scaloidal part of
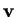
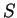
- level surface of arbitrary scalar field
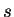
- mesh stretching factor in §5.1.5
-
- arbitrary scalar field in §2.6.1
- Sc
- Schmidt number,
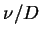
- Sh
- Sherwood number,
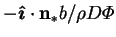
-
![$\mbox{$\mathcal T$}[\mathbf{v}]$](img70.png)
- scalar defining the toroidal part of
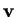
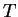
- reduced temperature,
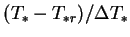
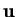
- reduced velocity,
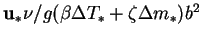
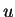
- reduced transverse component of velocity,
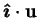
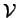
- term of an inner matched asymptotic expansion
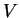
- volume enclosed by level surface,
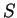
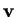
- arbitrary vector field

- reduced vertical component of velocity,
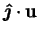
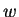
- reduced spanwise component of velocity,
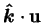
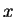
- reduced transverse coordinate,
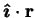
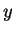
- reduced vertical coordinate,
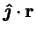
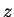
- reduced spanwise coordinate,
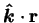
Greek symbols
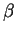
- thermal coefficient of cubic expansion
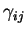
- component of metric tensor
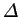
- inner gauge function in a matched asymptotic expansion
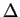
- characteristic difference
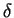
- outer gauge function in a matched asymptotic expansion
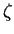
- vapour coefficient of cubic expansion
-
- stretched coordinate for region near front wall in §7.4.2
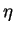
- spherical coordinate: colatitude,
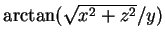
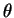
- spherical coordinate: colatitude,
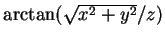
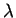
- thermal conductivity
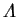
- latent heat factor,
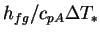
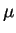
- (dynamic) viscosity
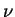
- kinematic viscosity
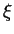
- stretched coordinate for region near hot wall
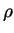
- density
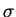
- function defined by (4.29),
appearing in (4.27)
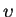
- spherical coordinate: azimuth,
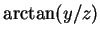
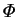
- mass transfer rate factor,
![$\ln[(1-m_{*r})/(1-m_{*r}-\Delta m_*)]$](img106.png)
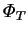
- thermal mass transfer rate factor,
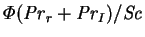
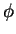
- spherical coordinate: azimuth,
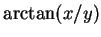
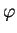
- test function for variational form of Navier-Stokes equation
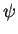
- vertical component of solenoidal vector potential for
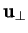
-
- Stokes's stream-function in §8.2
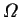
- rotational speed
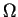
- domain, with boundary
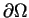
Superscripts

- unit magnitude

- mean

- transformed
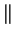
- in a domain with
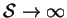
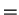
- in a domain with
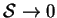

- in a domain with rectangular horizontal section
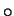
- in a domain with circular horizontal section
-
![\scalebox{1.414}[0.7071]{$\circ$}](img126.png)
- in a domain with elliptic horizontal section
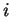
- contravariant component
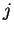
- contravariant component
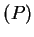
- poloidal part
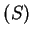
- scaloidal part
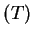
- toroidal part
Subscripts
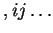
- covariant derivative with respect to
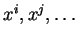
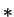
- dimensional
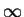
- fully developed
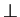
- restricted to a horizontal plane
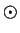
- restricted to a plane of constant
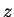
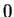
- at the wall
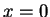
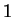
- at the wall
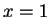
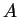
- species A, the vapour
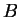
- species B, the gas

- forced
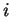
- Cartesian tensor component
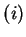
- species index in a multicomponent mixture
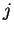
- Cartesian tensor component
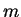
- pertaining to mass transfer or composition
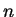
- natural
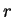
- at the reference state
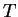
- thermal




Next: Introduction
Up: Vapour transport across gas-filled
Previous: Preface
Contents
Geordie McBain
2001-01-27