The fundamental lemma is due to Chadwick and Trowbridge (1967).
Vectors of the form
![]() and
and
![]() are called poloidal and toroidal,
respectively.
It has been shown by Backus (1986) that the lemma can be extended from
spherical annuli to spheres. The scalars can be obtained as the regular
solutions of
are called poloidal and toroidal,
respectively.
It has been shown by Backus (1986) that the lemma can be extended from
spherical annuli to spheres. The scalars can be obtained as the regular
solutions of
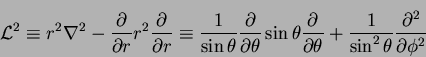 |
(B.3) |
The operator
![]() is the surface
Laplacian for the unit sphere (Aris 1989, pp. 196-7, 222).
Its eigenfunctions are the spherical harmonics:
is the surface
Laplacian for the unit sphere (Aris 1989, pp. 196-7, 222).
Its eigenfunctions are the spherical harmonics:
An immediate and extremely useful consequence of
(B.4) is
The spherical components of poloidal and toroidal fields are:
Clearly, arbitrary functions of ![]() may be added to
may be added to
![]() or
or
![]() without affecting
without affecting
![]() or
or
![]() (Moffatt 1978, p. 19).
(Moffatt 1978, p. 19).