Vorticity at the section centre

A convenient single scalar quantifying the effect of the end-walls on the flow in the plane of spanwise symmetry is the magnitude of the vorticity there. If $\omega$ is defined as the dimensionless vorticity, with scale $g(\beta\Delta T_*+\zeta\Delta m_*)b/\nu$, then for purely vertical flows,

$$\mbox{\boldmath$\omega$}= -\frac{1}{\mbox{$\mathcal S$}} \fr... ...th}$}+ \frac{\partial v}{\partial X}\mbox{\boldmath$\hat{k}$}.$$ (7.71)

At the centre $(X=Z=0)$ of an elliptic or rectangular section, the transverse ($X$-direction) component must vanish, since both $v_f$ and $v_n$ are even in $Z$. Thus, the vorticity at the centre is:

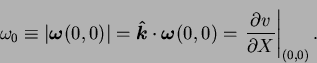$$\omega_0\equiv \left\vert\mbox{\boldmath$\omega$}(0,0)\right... ...0)= \left.\frac{\partial v}{\partial X}\right\vert _{(0,0)}.$$ (7.72)

For elliptic sections, and considering only the buoyancy-induced part of the flow, $v_n\!\!\raisebox{1ex}{\scalebox{1.414}[0.7071]{$\circ$}}$,

$$\omega_{n0}\!\!\!\!\!\!\raisebox{1ex}{\scalebox{1.414}[0.7071]{$\circ$}}\; = \frac{1}{8(3+\mbox{$\mathcal S$}^{-2})}.$$ (7.73)

For rectangular sections, using the series representation (7.25) for $v_n^{\Box}$, the vorticity at the section centre is:

$$\omega_{n0}^{\Box} = \omega_{n0}^{\Vert} + \frac{1}{2\upi ^2... ...nfty}\frac{(-1)^k}{k^2} \mathrm{sech}k\upi \mbox{$\mathcal S$}$$ (7.74)

where

$$\omega_{n0}^{\Vert} = \frac{1}{24}$$ (7.75)

is the asymptotic value for large $\mathcal S$. Series (7.74) is rapidly convergent and practical for all but extremely small values of $\mathcal S$. For these, the Hele-Shaw limit can be obtained from the limiting velocity profile for $\mbox{$\mathcal S$}\rightarrow 0$, equation (7.27):

$$\omega_{n0}^{\Box} \sim \frac{\mbox{$\mathcal S$}^2}{8}\qquad(\mbox{$\mathcal S$}\rightarrow 0)$$ (7.76)

The vorticity at the section centre is plotted from equations (7.73), (7.74), (7.75) and (7.76) in figure 7.7.

Figure 7.7: Vorticity due to buoyancy at the section centre. The Hele-Shaw limit is given by (7.76), and the Jones-Furry limit by (7.75).

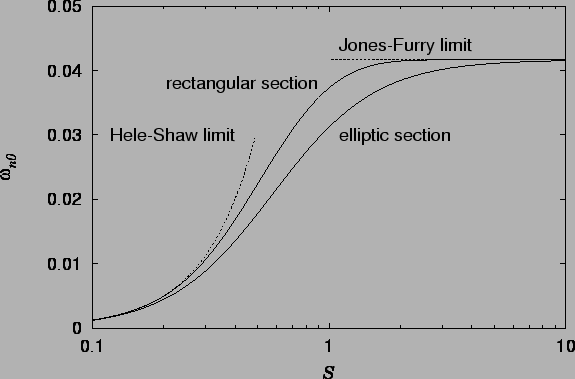Figure 7.7 shows that the vorticity in the central vertical line of a cavity or duct of elliptic section is always less than that in a rectangular duct of the same aspect ratio. This is because the `end-walls' are closer, on average, to the plane of spanwise symmetry in the elliptic section than in the rectangular section. Their viscous damping of the vertical flow is therefore greater.

For rectangular cavities, figure 7.7 confirms the validity of the estimate made in §7.4.3 that for $\mbox{$\mathcal S$}>1.7$ the flow in the plane $Z=0$ would be essentially the same as for $\mbox{$\mathcal S$}\rightarrow\infty$. The equivalent figure for the elliptic section is $\mbox{$\mathcal S$}>33^{1/2}\doteq 5.7$, the value being larger because of the stronger viscous damping from the `end-walls'.