



Next: The narrow cavity limit
Up: The Narrow Cavity Limit
Previous: Introduction
Contents
The two-dimensional equations
In terms of the Cartesian components of velocity and the normalized coordinates
(2.74), the conservation equations for the gas-vapour mixture
(2.52)-(2.55) are
and
Restricting attention for the moment (until chapter 7) to two
dimensions by considering only cavities very extensive in the spanwise
direction, in the limit
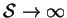 ; the above equations
(4.1)-(4.6) become
; the above equations
(4.1)-(4.6) become
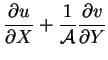 |
 |
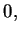 |
(4.7) |
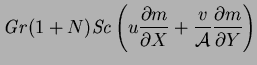 |
 |
 |
(4.8) |
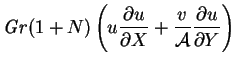 |
 |
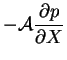 |
|
| |
|
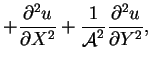 |
(4.9) |
 |
 |
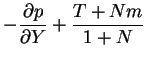 |
|
| |
|
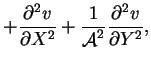 |
(4.10) |
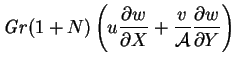 |
 |
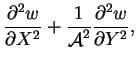 |
(4.11) |
and
It is seen that apart from (4.11),
none of the equations depend on 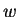 , so that
it may be ignored and (4.11) dropped; note that
, so that
it may be ignored and (4.11) dropped; note that 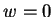 is a solution of the large
is a solution of the large 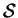 limit of the spanwise component of the
momentum equation
(4.11). It may then be assumed
that
limit of the spanwise component of the
momentum equation
(4.11). It may then be assumed
that 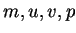 and
and 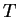 are independent of
are independent of 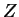 , so long as this is
consistent with the boundary conditions on all walls with the possible
exception of the front and
back walls, since these are now (
, so long as this is
consistent with the boundary conditions on all walls with the possible
exception of the front and
back walls, since these are now (
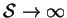 ) infinitely removed.
) infinitely removed.




Next: The narrow cavity limit
Up: The Narrow Cavity Limit
Previous: Introduction
Contents
Geordie McBain
2001-01-27

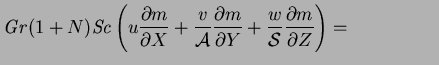
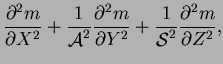
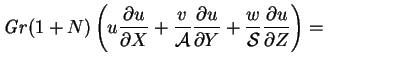
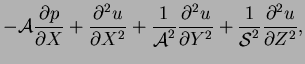

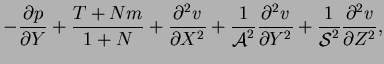
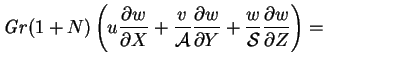
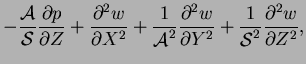
![]() ; the above equations
(4.1)-(4.6) become
; the above equations
(4.1)-(4.6) become