



Next: Extreme spanwise aspect ratios
Up: Narrow cavities with bounded
Previous: Numerical evaluation of the
Contents
Contours of the vertical component of velocity due to buoyancy, 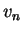 ,
calculated using (7.25) and (7.35)
are shown in figure 7.2,
,
calculated using (7.25) and (7.35)
are shown in figure 7.2,
Figure 7.2:
Fully developed buoyancy-induced flow in various rectangular
sections. Curves can be interpreted as either vortex-lines or
contours of the vertical component of velocity with
levels at 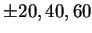 and
and  of maximum.
of maximum.
 and
and  mark extrema of
mark extrema of 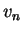 (points of
zero vorticity).
(points of
zero vorticity).
![\begin{figure}\setlength{\unitlength}{1mm}\begin{center}
\begin{picture}(110,96)...
...{\makebox(0,0)[t]{$z$}}
\end{picture}}
\par\end{picture}\end{center}\end{figure}](img846.png) |
in the unnormalized coordinates 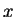 and
and 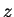 . The curves can be
interpreted as either contours of
. The curves can be
interpreted as either contours of 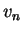 or vortex-lines, since the gradient
of velocity in the
or vortex-lines, since the gradient
of velocity in the 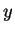 -direction is zero (see Theorem 3,
p.
-direction is zero (see Theorem 3,
p. ![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) ).
).
Geordie McBain
2001-01-27
![]() ,
calculated using (7.25) and (7.35)
are shown in figure 7.2,
,
calculated using (7.25) and (7.35)
are shown in figure 7.2,
![\begin{figure}\setlength{\unitlength}{1mm}\begin{center}
\begin{picture}(110,96)...
...{\makebox(0,0)[t]{$z$}}
\end{picture}}
\par\end{picture}\end{center}\end{figure}](img846.png)