Trevisan and Bejan (1987) considered vapour transport across a plane vertical
rectangular cavity at low mass transfer rates (
![]() ).
Uniform flux boundary conditions were imposed at the hot and cold walls.
Exact solutions were reported for infinitely tall cavities
(
).
Uniform flux boundary conditions were imposed at the hot and cold walls.
Exact solutions were reported for infinitely tall cavities
(
![]() ) at large combined Grashof numbers,
) at large combined Grashof numbers,
![]() ,
for three limiting cases:
,
for three limiting cases:
![]() ;
;
![]() ,
,
![]() ; and
; and
![]() ,
,
![]() . The first of these is actually not
quite exact, in that it assumes that there exists a stagnant stratified core
between the boundary layers on the walls, so that the transverse length
scale of the flow near the hot and cold walls is much smaller than the breadth
of the cavity;
it is therefore equivalent to Prandtl's (1952, p. 422; Elder 1965; Gill 1966)
solution for heat transfer from a single wall to an unbounded pure fluid.
A solution valid across the breadth of the cavity was given
independently by Vest and Arpaci (1969) and Aung (1972).
The paper also contains numerical solutions for
. The first of these is actually not
quite exact, in that it assumes that there exists a stagnant stratified core
between the boundary layers on the walls, so that the transverse length
scale of the flow near the hot and cold walls is much smaller than the breadth
of the cavity;
it is therefore equivalent to Prandtl's (1952, p. 422; Elder 1965; Gill 1966)
solution for heat transfer from a single wall to an unbounded pure fluid.
A solution valid across the breadth of the cavity was given
independently by Vest and Arpaci (1969) and Aung (1972).
The paper also contains numerical solutions for
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
Trevisan and Bejan offered a simple scaling argument to determine when
transpiration could be neglected for ![]() and
and
![]() .
Their result was that this is safe when
.
Their result was that this is safe when
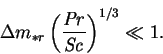 |
(3.1) |
| (3.2) |