



Next: Literature Review
Up: Some properties of the
Previous: The nonexistence of hydrostatic
Contents
An invariance property
It should be expected on physical grounds that the system is invariant in
some sense if the `cold' and `hot' walls are renamed; i.e. if one looks at the
same cuboid from behind.
This is most easily seen if the governing equations are expressed in tensor
form. For definiteness, consider uniform vapour mass fraction and temperature
on the cold and hot walls and let the other four walls of the cuboid be
perfectly conducting and impermeable. As usual, all walls are assumed to be
non-slip. With the contravariant coordinates
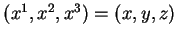 ,
(2.52)-(2.55) can be rewritten:
,
(2.52)-(2.55) can be rewritten:
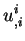 |
 |
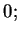 |
(2.94) |
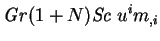 |
 |
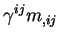 |
(2.95) |
 |
 |
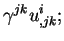 |
(2.96) |
![$\displaystyle \mbox{\textit{Gr}}(1+N)\left[
\mbox{\textit{Pr}}_r + \mbox{\textit{Pr}}_I\left(1-\mathrm{e}^{-\varPhi }\right)m
\right] u^i T_{,i}$](img370.png) |
|
|
|
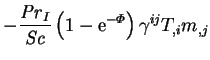 |
 |
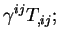 |
(2.97) |
where subscripts and superscripts refer to covariant and contravariant
components, respectively, and subscripts following a comma indicate
covariant differentiation. Summation over indices appearing in both upper
and lower positions in a term is understood.
(See, for example, Aris 1989, ch. 7, for a summary of tensor calculus).
The inhomogeneous boundary conditions are:
at 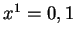 and
and
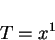 |
(2.100) |
on the other four walls.
The components of the
metric tensor, 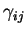 , are unity on the diagonal and zero otherwise for
this coordinate system;
therefore, since
, are unity on the diagonal and zero otherwise for
this coordinate system;
therefore, since 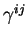 denotes the
denotes the 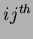 element of the inverse of
the matrix of
element of the inverse of
the matrix of 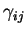 ,
,
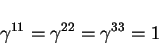 |
(2.101) |
and
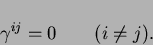 |
(2.102) |
The transformation discussed above is:
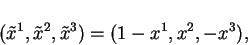 |
(2.103) |
which leaves the metric tensor unchanged, since it is only a rigid rotation
and translation of the coordinate axes.
The solution to the new system in terms of the solution of the old system is
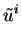 |
 |
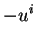 |
(2.104) |
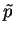 |
 |
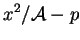 |
(2.105) |
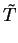 |
 |
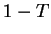 |
(2.106) |
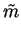 |
 |
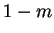 |
(2.107) |
if
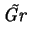 |
 |
 |
(2.108) |
 |
 |
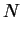 |
(2.109) |
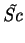 |
 |
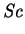 |
(2.110) |
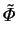 |
 |
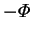 |
(2.111) |
 |
 |
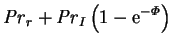 |
(2.112) |
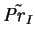 |
 |
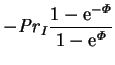 |
(2.113) |
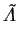 |
 |
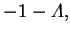 |
(2.114) |
which agrees with the result that would be deduced by transforming the
parameters according to their definitions in terms of the physical
properties and boundary conditions.
The Sherwood and Nusselt numbers are given by
so that
The Nusselt number does not transform as simply as the Sherwood number as
the driving force for energy transfer, unlike that for mass transfer, cannot
be written in terms of a function of a single property at the boundaries;
energy transfer is driven by both the temperature difference and the
mass transfer. If 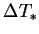 had been taken as the
driving force for energy, then the `Nusselt number'
had been taken as the
driving force for energy, then the `Nusselt number'
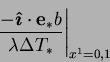 |
(2.119) |
would be an invariant of the transformation, like the Sherwood number. As will
be seen in chapters 4-6, however, this would lead to
the value of the Nusselt number depending more strongly on the thermal
mass transfer rate factor,  .
.
When 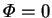 , the transformation of the parameters simplifies to
, the transformation of the parameters simplifies to
and
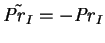 , although the interdiffusion Prandtl number is then
irrelevant. In this case, both the Sherwood and Nusselt numbers are invariants
of the transformation.
, although the interdiffusion Prandtl number is then
irrelevant. In this case, both the Sherwood and Nusselt numbers are invariants
of the transformation.
The significance of the present findings lies in what they reveal about the
symmetry of the Sherwood and Nusselt numbers with respect to the parameters
of the problem. This should be exploited when constructing the functional
form of correlations, for example. An instance of this will be found in
§8.2.10, when the behaviour of the system at low Grashof
number is examined.
Also, the simplicity of the
symmetry of Sh with respect to 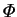 is one advantage
of using
is one advantage
of using 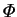 as the parameter representing finite mass transfer effects;
this becomes important when considering a rational approximation for the
system at low mass transfer rates (ch. 6, see especially
§,6.2.2).
as the parameter representing finite mass transfer effects;
this becomes important when considering a rational approximation for the
system at low mass transfer rates (ch. 6, see especially
§,6.2.2).




Next: Literature Review
Up: Some properties of the
Previous: The nonexistence of hydrostatic
Contents
Geordie McBain
2001-01-27
![]() ,
(2.52)-(2.55) can be rewritten:
,
(2.52)-(2.55) can be rewritten:

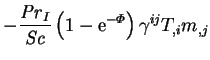
![$\displaystyle \frac{1-\mathrm{e}^{-\varPhi }}
{\mbox{\textit{Gr}}(1+N)\mbox{\te...
...eft[\left(1-\mathrm{e}^{-\varPhi }\right)m-1\right]}
\gamma^{ij}x^1_{,i} m_{,j}$](img376.png)
![]() , are unity on the diagonal and zero otherwise for
this coordinate system;
therefore, since
, are unity on the diagonal and zero otherwise for
this coordinate system;
therefore, since ![]() denotes the
denotes the ![]() element of the inverse of
the matrix of
element of the inverse of
the matrix of ![]() ,
,
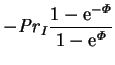
![$\displaystyle -\frac{\mbox{\textit{Gr}}(1+N)}{\varPhi }x^1_{,j} u^j =
\frac{1-\...
...left[1-m\left(1-\mathrm{e}^{-\varPhi }\right)\right]}
\gamma^{ij}x^1_{,j}m_{,i}$](img405.png)
![$\displaystyle \frac{1-\mathrm{e}^{-\varPhi _T}}{\varPhi _T}
\left[ \gamma^{ij}x^1_{,j} T_{,i} + (T+\varLambda ) \varPhi _T \mbox{\textit{Sh}}\right]$](img406.png)
![]() had been taken as the
driving force for energy, then the `Nusselt number'
had been taken as the
driving force for energy, then the `Nusselt number'
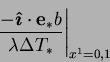
![]() , the transformation of the parameters simplifies to
, the transformation of the parameters simplifies to
![]() is one advantage
of using
is one advantage
of using ![]() as the parameter representing finite mass transfer effects;
this becomes important when considering a rational approximation for the
system at low mass transfer rates (ch. 6, see especially
§,6.2.2).
as the parameter representing finite mass transfer effects;
this becomes important when considering a rational approximation for the
system at low mass transfer rates (ch. 6, see especially
§,6.2.2).