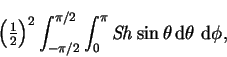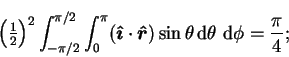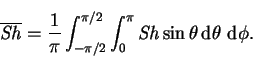Next: Conclusions
Up: Spherical enclosures
Previous: Flow structure to first
Contents
Overall vapour and energy transfer rates
The definition of the Sherwood number for the cuboid, (6.21),
is here modified for the sphere:
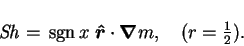 |
(8.76) |
The net flux through the hemispherical surface
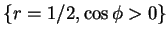 is
is
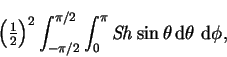 |
(8.77) |
which is equal to the net flux through the disk, 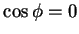 (i.e. the
(i.e. the  plane) or the other hemispherical surface:
plane) or the other hemispherical surface:
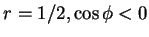 . The Sherwood number is averaged by dividing the common
net flux through these surfaces by the projection of their area in the
. The Sherwood number is averaged by dividing the common
net flux through these surfaces by the projection of their area in the
 -plane,
-plane,
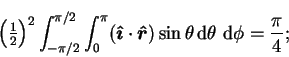 |
(8.78) |
thus
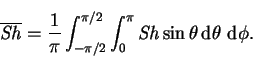 |
(8.79) |
To first order in Gr,
The first order correction to the mean Sherwood number vanishes because 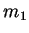 is an odd
function of
is an odd
function of 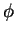 . The increased diffusion in the quadrants
. The increased diffusion in the quadrants 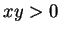 is balanced by the lower rate in the other two quadrants. The first order
correction to the Sherwood number may also have been expected to vanish
from more general symmetry considerations:
is balanced by the lower rate in the other two quadrants. The first order
correction to the Sherwood number may also have been expected to vanish
from more general symmetry considerations:
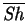 should be an even
function of
should be an even
function of
 (§2.6.3).
(§2.6.3).
The results for the energy transfer rate are completely analogous.




Next: Conclusions
Up: Spherical enclosures
Previous: Flow structure to first
Contents
Geordie McBain
2001-01-27