The single fluid heat transfer problem

In discussing various hydrodynamic features of the present problem, I shall often have cause to refer to the `analogous single fluid heat transfer problem', for which there exists an extremely extensive body of literature; see Gebhart et al. (1988, pp. 737-52), Ostrach (1988) or Bejan (1995, ch. 5) for a review.

To facilitate this, its equations are derived here; this being briefly accomplished since they are merely a limiting case of the present set, formed by setting the vapour mass fraction difference, $\Delta m_{*}$, to zero (i.e. $\varPhi =N=0$) in the equations of motion (2.54) and energy (2.55):

$$\mbox{\textit{Gr}}\,\mathbf{u}\cdot\mbox{\boldmath$\nabla$}\mathbf{u} = -\mbox{\boldmath$\nabla$}p+T\mbox{\boldmath$\hat{\jmath}$}+\mbox{\boldmath$\nabla$}^2\mathbf{u};$$ (2.69)

$$\mbox{\textit{Gr}}\mbox{\textit{Pr}}_r\mathbf{u}\cdot\mbox{\boldmath$\nabla$}T = \nabla^2T.$$ (2.70)

It is clear that these equations are uncoupled from the equation of continuity of the diffusing species (2.53), which may therefore be dropped. The equation of continuity of the `mixture' (2.52) is unchanged. The Nusselt number (2.66) becomes

$$\mbox{\textit{Nu}}= \mbox{\boldmath$\hat{\imath}$}\cdot\mbox{\boldmath$\nabla$}T,$$ (2.71)

since

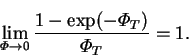$$\lim_{\varPhi \rightarrow 0}\frac{1-\exp(-\varPhi _T)}{\varPhi _T}=1.$$ (2.72)

The product $\mbox{\textit{Gr}}\mbox{\textit{Pr}}_r$ is frequently called the Rayleigh number, Ra.