



Next: STATEMENT OF SOURCES
Up: Vapour transport across gas-filled
Previous: Contents
Contents
- Cuboid domain geometry
- Vapour transfer in a plane vertical square cavity
- Energy transfer in a plane vertical square cavity
- Profiles of
 and
and 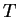 in the narrow cavity limit
in the narrow cavity limit
- Profiles of
 in the narrow cavity limit
in the narrow cavity limit
- Variation of
 with
with 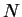 in the narrow cavity limit
in the narrow cavity limit
- Variation of
 with
with 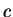 in the narrow cavity limit
in the narrow cavity limit
- Geometry and boundary conditions for Fastflo solutions
- Vinokur's (1983) symmetric stretching function
- A typical mesh for the Fastflo solutions
- A sample Fastflo solution
- Processed solution variables in Fastflo
- Energy flux components
- Energy transfer in the cavity: vectors and `heat-lines'
- Contour plots from two Fastflo runs
- Discrepancies between the Fastflo and analytic solutions
- The effect of
 on the conduction-diffusion regime
on the conduction-diffusion regime
- Penetration of convective effects into the core
- Geometry for cavities of rectangular section
- Fully developed buoyancy-induced flow
- Stretched coordinates for regions near walls
- The effect of the end-walls
- Geometry for elliptic sections.
- Fully developed buoyancy-induced flow in elliptic sections
- Vorticity due to buoyancy at the section centre
- Buoyancy-induced flow in the spanwise symmetry plane
- Velocity maximum in rectangular sections
- Cartesian axes for the spherical cavity
- Temperature in the surrounding solid
- Decomposition of a vector field
- Zeroth order pressure
- First order vapour mass fraction or temperature
- Mass fraction or temperature to first order
- First order stream-lines due to inertia
- First order pressure due to inertia
- First order stream-lines due to buoyancy
- First order pressure due to buoyancy
- Three-dimensional stream-lines in a spherical cavity
- Three-dimensional stream-lines in a spherical cavity (cont.)
Geordie McBain
2001-01-27