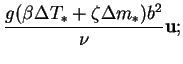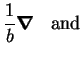Next: Mass and energy fluxes
Up: Basic Equations of Vapour
Previous: Heat and mass transfer
Contents
Nondimensionalization
The primitive dependent variables are reduced to dimensionless form by:
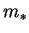 |
 |
 |
(2.26) |
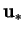 |
 |
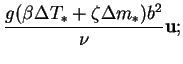 |
(2.27) |
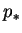 |
 |
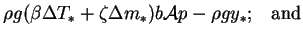 |
(2.28) |
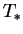 |
 |
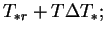 |
(2.29) |
where 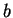 is a characteristic length of the domain
and
is a characteristic length of the domain
and 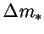 and
and 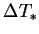 are
characteristic differences of vapour mass fraction and temperature, to be
introduced by the boundary conditions, respectively.
Also,
are
characteristic differences of vapour mass fraction and temperature, to be
introduced by the boundary conditions, respectively.
Also,
where 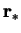 is the position vector.
is the position vector.
The scales in this scheme were chosen to ensure that the variables have values
of order unity in the solutions later obtained (ch. 4,
7, 8). In general, these are
characterized by a dominance of the diffusive (including conduction and
viscous diffusion of momentum) as opposed to the advective terms in the field
equations.
Subsections




Next: Mass and energy fluxes
Up: Basic Equations of Vapour
Previous: Heat and mass transfer
Contents
Geordie McBain
2001-01-27