Omissions in the species equation

Other contributions to the diffusion flux, 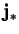$\mathbf{j}_*$, are (Bird et al. 1960, p. 567):

• pressure diffusion, which is only important for tremendous pressure gradients, as in centrifuges;
• forced diffusion, which is only relevant when the net external force per unit mass differs from species to species, as in electrochemical systems; and
• the Soret effect, which is only important for very steep temperature gradients, as in Clusius-Dickel columns (Jones & Furry 1946), or for gas-vapour mixtures with very different molecular weights (Abernathy & Rosenberger 1981).

Although large temperature differences and vapour mixtures including some very heavy species are occasionally employed in crystal growth systems (see, for example, Evans & Greif 1998), neither the temperature nor pressure gradients can be very large in a building wall cavity. Further, the ratio of the molecular weights of water vapour and atmospheric air (considered as a single gas), 0.62, is almost unity compared to those encountered by Abernathy and Rosenberger (1981), 32.8 and 3.28, or Evans and Greif (1998), 11.0.

With the temperature and mass fraction varying through the cavity, supersaturation of the vapour is possible. Whether or not this leads to condensation in the body of the cavity, and, if so, at what rate droplet formation and growth proceed, depends on the presence, nature and distribution of nucleating aerosols. An analysis of these molecular kinetics lies outside the scope of continuum fluid mechanics and this project. The physics is described in the meteorological treatises of Fletcher (1962, ch. 3) and Rogers and Yau (1989, ch. 6) and summarized in chapter 3 of my B.E. thesis (McBain 1995).

If condensation takes place only at the boundaries, the steady-state species equation can be written in divergence form with no source or sink terms, as above (2.5).

A simple way of investigating the effect of the condensation within the gas-vapour phase on the overall energy transfer rate is to solve the system of equations assuming each of two extreme possibilities:

1. No aerosols are available for heterogeneous nucleation, in which case the species and energy equations are as above--homogeneous nucleation occurring only at very high supersaturations; e.g. relative humidity in excess of 400% for water vapour at normal temperatures (McBain 1995).
2. Aerosols perfectly suitable for heterogeneous nucleation are abundant, so that the mixture cannot sustain any degree of supersaturation.

In the latter case, provided the gas-vapour mixture is saturated at its boundaries, the analogy developed by Close and Sheridan (1989) and verified by Close et al. (1991) becomes available, and the overall energy transfer rate can be predicted from single fluid heat transfer correlations, with modified properties. I carried out such an investigation as part of my B.E. thesis (McBain 1995). The results, reported therein and by McBain, Harris, Close and Suehrcke (1998), indicated that condensation within the gas-vapour phase led to higher overall energy transfer rates, particularly at higher mean temperatures. The greatest increase, 8%, was found at the highest mean temperature, 50$\circ$C.

The problem of condensation of the vapour away from the boundaries is very important in the growth of crystals by PVT, where saturated boundary conditions are the norm, as it can lead to `morphological instability' of the growth face (Faktor & Garrett 1974, pp. 216-7; Rosenberger et al. 1997).

The present work is restricted to the case where the vapour only condenses at the boundaries, a case which will certainly prevail if the gas-vapour mixture is everywhere unsaturated. The basic equations presented in this chapter ignore the degree of saturation (relative humidity for air-water vapour systems). The solutions of these equations will be valid if, for a particular dimensional set of values of the boundary conditions, the predicted degree of saturation is everywhere less than unity. Since the most likely cause for this not being the case in practice is that the vapour is saturated at the boundaries (so that the Close-Sheridan analogy is applicable), this is not a very serious restriction. I have no recommendations on how to treat cases of mixed saturation and unsaturation, except to say that, based on the study cited above, the present methods neglecting vapour-phase condensation should give a reasonable approximation of the overall mass and energy transfer rates.